Qué es la econometría

En el complejo mundo económico, en el que nos movemos hoy en día, se hace vital, para el correcto funcionamiento del sistema, las predicciones económicas y la fiabilidad que estas presenten. Para realizar estas labores, la economía se deriva en una rama denominada econometría.

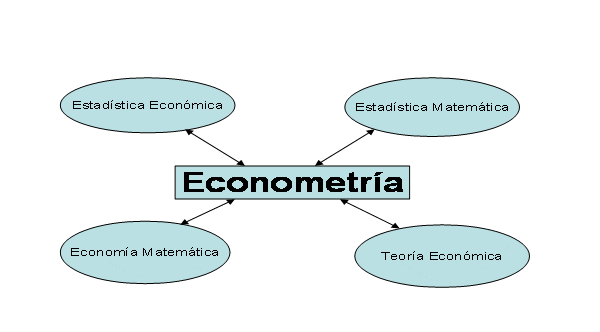
Podemos dar una definición de la econometría como la rama de la economía que se vale de modelos matemáticos y estadísticos, de la programación lineal y la teoría de juegos; para analizar, interpretar y hacer predicciones en la economía, prediciendo variables vitales para la misma como el precio, las reacciones del mercado, el coste de producción o las consecuencias de las políticas económicas.

¿QUÉ ES LA ECONOMETRÍA?

Muchos han sido los autores que han tratado de explicar esta ciencia económica para tratar de hacerla más comprensible tanto para los economistas, como para el resto de los ciudadanos. Una de mis preferidas es la siguiente:

‘La econometría es la rama más operativa de la Ciencia económica. Trata de representar numéricamente las relaciones económicas mediante una adecuada combinación de la Teoría económica matemática y la Estadística. De forma que las matemáticas, como lenguaje y forma de expresión simbólica e instrumento eficaz en el proceso deductivo, representan el medio unificador. Teoría económica, economía matemática o estadística económica serían consideraciones parciales de su contenido.’ (A.G. Barbancho – 1962)

No es fácil llegar a comprender en profundidad un sistema econométrico, ya que no basta con tener nociones de economía, sino que requiere unos profundos conocimientos de métodos estadísticos. A continuación os dejo una serie de vídeos que componen un curso online sobre econometría aplicada, para quien quiera profundizar más en la materia:

 

MODELO ECONOMÉTRICO

Para la obtención de un modelo econométrico se utiliza el denominado “Método de los mínimos cuadrados (MCO)“, también denominada “Teoría de la regresión lineal“.

Comenzaremos representando las relaciones entre una variable que queremos conocer o variable endógena (Y) y otras variables dependientes que la determinan (X1 hasta Xn), denominadas variables exógenas, de la siguiente manera:

El objetivo del modelo econométrico es obtener los valores de los parámetros desde 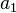hasta .

El modelo se completa añadiendo un término más, llamado término independiente (β0), que es un parámetro constante más a buscar. Así:

.

Resulta conveniente, estadísticamente, suponer que siempre existe una constante dentro del modelo, para así poder contrastar la hipótesis de si es distinta, o no, de cero.

APLICACIONES DE LA ECONOMETRIA

Sabiendo cómo funciona el modelo económetrico, lo ideal, al menos para el lector no familiarizado con el análisis matemático sería conocer las utilidades de la econometría para la vida diaria, tanto a nivel de la política económica como de las decisiones empresariales. Cuatro conceptos lo van a aclarar:

• El análisis económico estructural ayuda a saber el comportamiento de la economía.
• La predicción de valores económicos.
• La planificación de actividades en función de las posibilidades de medición de las variables económicas establecidas.
• El control de valores óptimos de cualquier variable, gracias a las simulaciones, aplicables tanto a la empresa como a la política económica de un país.

MODELO NO DETERMINISTA

La relación entre variables endógenas y exógena no es del todo determinista, esto quiere decir que por mucho que lo intentemos, siempre existirá cierto grado de error aleatorio. Esto significa que el modelo sobreentiende que está excluyendo a todas aquellas variables que no se hayan podido incluir (normalmente por su escaso aporte proporcional a la relación), pero que también tienen cierta influencia. Esto se le añade al modelo, representado en forma de variable aleatoria (μ):

Para poder utilizar esta variable se debe suponer que es una variable aleatoria normal, con media cero y varianza constante en todas las muestras.

El Modelo de regresión lineal presenta una serie de problemas que la estadística trata de solucionar, para lograr el objetivo de entender las relaciones existentes entre los diferentes factores que influyen en la economía.

Para entender, a nivel microeconómico cómo se entenderían estos modelos, supongamos que un@ am@ de casa quiere saber, qué y cómo influye en la cantidad de veces que compra carne para comer a lo largo de un mes. En este caso la cantidad de carne comprada sería la variable endógena (Y), qué es la que queremos conocer. Para comprar esa carne debe tener dinero para comprarla, lo cual consideremos que su salario es constante, en este caso dicho salario sería (β0). La idea del modelo es que aquí influirían factores como por ejemplo el precio de ese mes de varios productos sustitutivos, como la verdura, el pescado, etc., o bien cuantos imprevistos haya tenido a lo largo de ese mes. Estas variables serían los (X1, X2,…,Xn). Y que influyen en mayor o menor medida de sus respectivos valores, en este caso representados por (β1, β2,…,βn). Además para finalizar se deben incluir de forma residual factores con aparente poca, pero existente, influencia en la decisión de compra de la carne, como puede ser la climatología, el tiempo disponible para hacer la compra, etc.

Desarrollando el modelo hasta el final, y obteniendo los estadísticos pertinentes, podríamos llegar a delimitar la fiabilidad con la que este modelo de regresión lineal es capaz de explicar la decisión de compra de la carne, o de cualquier otra decisión humana dentro de la economía. Algo que puede parecer a priori impredecible, pero que los modelos económicos, a través de la estadística se encarga de tratar de demostrar. Algo que puede ser de interés en términos macroeconómicos, pero también es de interés para las empresas y los agentes económicos. Las estadísticas pueden aportar a la microeconomía datos históricos y previsiones que faciliten la gestión empresarial.

Ese es el principal objetivo de los economistas hoy en día, hacer predicciones fiables de lo que va a ocurrir en el futuro, en función de cómo se espera que evolucionen las diferentes variables con trascendencia en la economía.